Reflection
Most objects we encounter have some form of symmetry. This means that we can build half of what we want, or even less, if we can then simply reflect it. In this Tutorial we will learn how to use ShapeJS's built in symmetry functions in order to modify data sources.
1. Planar Reflection
Let's start by modeling the beginnings of a toy car.
function main(args) {
var r = 15*MM;
var sphere = new Torus(r, r/5);
var box = new Box(0,0,0, 1.5*r,1.5*r, 1.5*r);
var shape = new Add(sphere,box);
var s = 26*MM;
return new Scene(shape,new Bounds(-s,s,-s,s,-s,s));
}
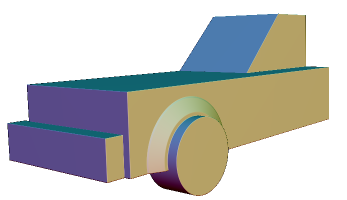
Now, we could repeat all the same operations, creations, and so forth on the other side. And then do both to make the rear end of the car. What we would be doing is manually creating reflections. But there is a much simpler way: using planar reflect. However, we need multiple reflections: once over the Z axis, and once over the X axis. Fortunately, we can combine multiple planar reflections into a single transformation. We'll also get another shot at creating a function. By doing this, we can create the whole car while only really modeling a fourth of it. Everything we are doing here should be familiar, except for this ReflectionSymmetry operation.
By using it we can avoid having to do any more modeling. Instead, we just create two planes, one along the X axis, one along the Z. We then apply this like any other transformation in order to get a more complete vehicle, rather than a single seater circle driver.
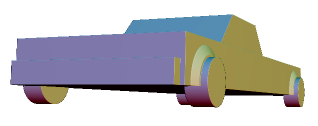
function main(args) {
var r = 15*MM;
var sphere = new Torus(r, r/5);
var box = new Box(0,0,0, 1.5*r,1.5*r, 1.5*r);
var shape = new Add(sphere,box);
var s = 26*MM;
return new Scene(shape,new Bounds(-s,s,-s,s,-s,s));
}
(Note: for a simpler reflections that only require a single transform, rather than having to set up an array, try using PlaneReflection.)
2. Circular Reflection
Beyond the basic planar reflection, we can also reflect a data source on a sphere. You can find a bit more technical explanation by reading about the Riemann sphere. Essentially what this will do is reflect your object on a spherical surface
Meanwhile, we have a fairly boring car. Let's take it and make it into the Fractalmobile by adding a spherical reflection.
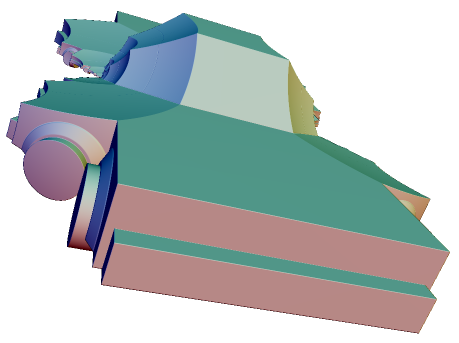
function quadSymmetry(){
var reflection_plane = new Array();
var count = 0;
reflection_plane[count++] = new ReflectionSymmetry.getPlane(new Vector3d(0,0,-1),0);
reflection_plane[count++] = new ReflectionSymmetry.getPlane(new Vector3d(-1,0,0),0);
reflection_plane[count++] = new ReflectionSymmetry.getSphere(new Vector3d(10*MM, 0, 0), -9*MM);
return new ReflectionSymmetry(reflection_plane);
}
function main(args) {
var chassisbase = new Box (2*MM, 0, 5*MM, 4*MM, 2*MM, 10*MM);
var chassisangle = new Plane (new Vector3d(4*MM, 1*MM, 10*MM), new Vector3d(3*MM, -1*MM, 10*MM), new Vector3d(4*MM, 1*MM, 10*MM));
var chassis = new Intersection(chassisbase, chassisangle);
var topbase = new Box (1.5*MM, 2*MM, 2*MM, 3*MM, 2*MM, 4*MM);
var topangle = new Plane (new Vector3d(0, 1*MM, 4*MM), new Vector3d(3*MM, 1*MM, 4*MM), new Vector3d(3*MM, 3*MM, 2*MM));
var top = new Intersection(topbase, topangle);
var bumperbase = new Box (1.8*MM, -0.5*MM, 10.25*MM, 4*MM, 1*MM, 0.5*MM);
var wheelbase = new Cylinder (new Vector3d(3.5*MM, -0.8*MM, 8*MM),new Vector3d(4.5*MM, -0.8*MM, 8*MM), 1*MM);
var fenderbase = new Cylinder (new Vector3d(4*MM, -0.8*MM, 8*MM),new Vector3d(4.2*MM, -0.8*MM, 8*MM), 1.5*MM, 1.1*MM);
var fender = new Subtraction(fenderbase, new Cylinder(new Vector3d(0, -1*MM, 0), new Vector3d(0, -1, 0), 1));
//
var car = new Union();
car.add(chassis);
car.add(top);
car.add(bumperbase);
car.add(wheelbase);
car.add(fender);
car.setTransform(quadSymmetry());
//
var s=15*MM;
return new Scene(car,new Bounds(-s,s,-s,s,-s,s));
}
(Note: With spherical reflections it can be hard to keep track of minimum thickness or ensure that you end up with only one piece. For more information on how to deal with this sort of problem, look at the 3D Import and Export Tutorial.)
It is very easy to add in more reflections since we have it set up as an array. Go ahead and give that a try. Who knows what you'll end up with?
